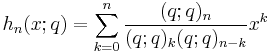Rogers–Szegő polynomials
Not to be confused with Rogers polynomials.
In mathematics, the Rogers–Szegő polynomials are a family of polynomials orthogonal on the unit circle introduced by Szegő (1926), who was inspired by the continuous q-Hermite polynomials studied by Leonard James Rogers. They are given by
where (q;q)n is the descending Pochhammer symbol.
References
- Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR2128719
- Szegő, Gábor (1926), "Beitrag zur theorie der thetafunktionen", Sitz Preuss. Akad. Wiss. Phys. Math. Ki. XIX: 242–252, Reprinted in his collected papers